一、点云(Point Cloud)
点云是一种3D数据,在文件里的表示方法其实就是一个一维向量:(x,y,z),还有可能是(x,y,z,Nx,Ny,Nz)N是法向量的意思。但它实际是空间中的一点,这一点来自激光雷达(Lidar)的扫描结果(个人猜测:其实就是发射若干个激光,根据反射回来的时间来计算出距离,这样,能定位出某一点的数据坐标)
点云数据的特征:无序性、点间关联、变换下的不变性。
(1)无序性:点云数据中,每一个向量都独立地表示空间的一个点,因此不论是哪一个点先被输入,都不影响最后点云数据的整体。
(2)点间关联:点的位置表示虽然独立,但是点与点之间存在着一些关系。因为一个点及其周围的点共同组成了物体的一部分,这种关系可以被提取出作为特征。
(3)变换下的不变性:这个变换特指“刚性变换(rigid motions)” 就是说将点云整体进行平移、旋转这种只改变位置而不改变形状大小的变化。在这种刚性变化下,点与点之间的距离位置关系是不变的,就像我转身、行走,都不会改变我的心脏与肺的位置关系。
二、目标分类(objection classification)与语义分割(segmentic segmentation)
目标分类与语义分割是两种不同粒度下的分类方式。前者是对单个物体进行识别分类,后者是对一个大的场景、对多个种类的物体进行分类。此外,还有一种叫部件分割(Part segmentation ),语义分割是对物体的整体进行分类,而部件分割是对一个物体的不同组成部分进行分类,如:飞机由机翼、机身、尾翼、发动机...组成
对于目标分类,输入有两种:1. 直接从点云数据中采样 2.使用某一场景点云中的预分割数据。对于第一种,是比较纯粹经典的,这种数据基本是单个物体、没有背景噪声;对于第二种,一般是在大规模场景中分割出一个子点云空间,然后根据这个子空间来作为输入,这种包含更多不同种物体,而且也会有噪声。其输出是一个k维向量,k是物体种类数量。
对于语义分割,输入也有两种:1. 对单个物体进行部件区域分割 2.在一个来源于3D空间的子空间上进行物体区域分类。前者是对一个物体的多个组成部分进行分类,而后者是在一个大的场景中对多种物体进行分类。语义分割的输出是一个n*m的size,n是点的数量,m是种类的数量。
三、传统的排序方法
传统排序方法是将点云数据按照一维的方式排列,这样存在一个问题,即:当点存在扰动的时候,可能会使得点在一维的顺序改变,从而使得训练模型认为物体形状发生了变化。有一个好理解的例子:若将点以x为标准进行一维化,得到(A,B,C,...)。但当点云数据存在扰动,使得B稍微偏移,最终可能得到的结果是(A,C,B,...),但在3维空间中,其形状并没有发生改变,但因为3维转换到1维后会丢失信息,因此模型会认为形状发生了变化。
四、PointNet
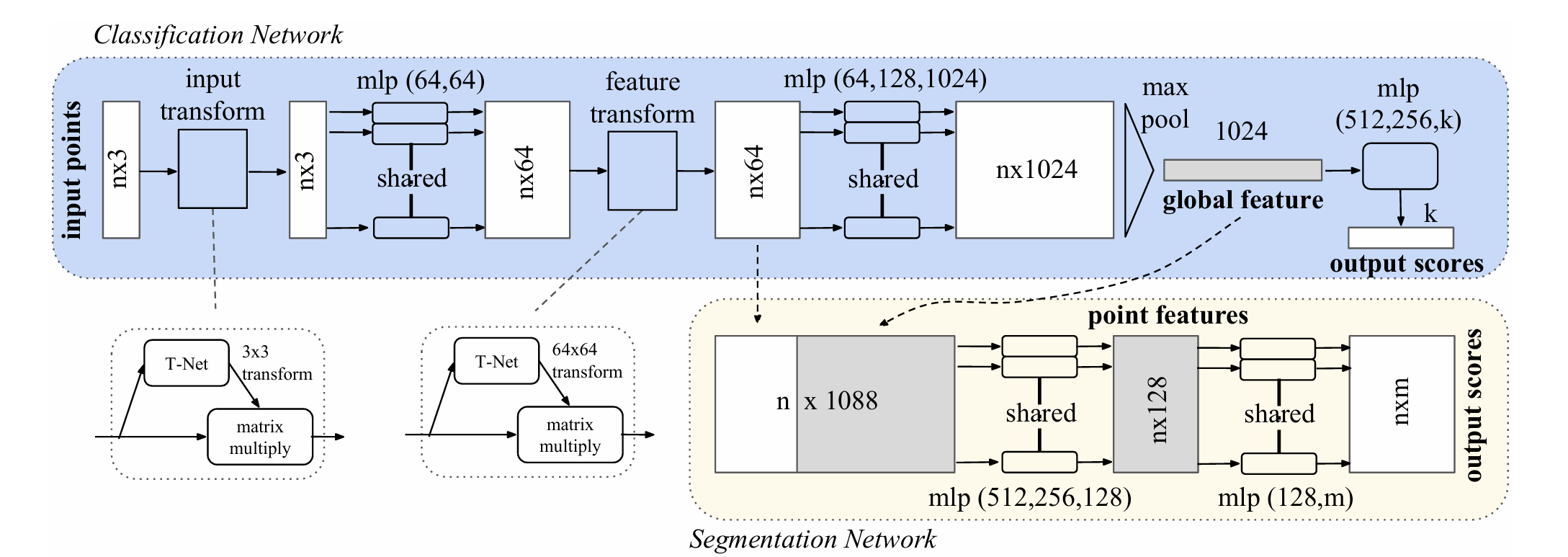
(1)无序数据的对称函数(Symmetry Function)
在说明了上述传统排序方法存在的问题后,PointNet则希望直接使用3D数据进行学习,而不是转换为低维度后进行处理。为了保证无序数据的输入排列不变(也就是说,不论输入顺序是怎样的,都不会影响模型的最终结果),作者提出用一种对称函数来实现输入排列的不变性。
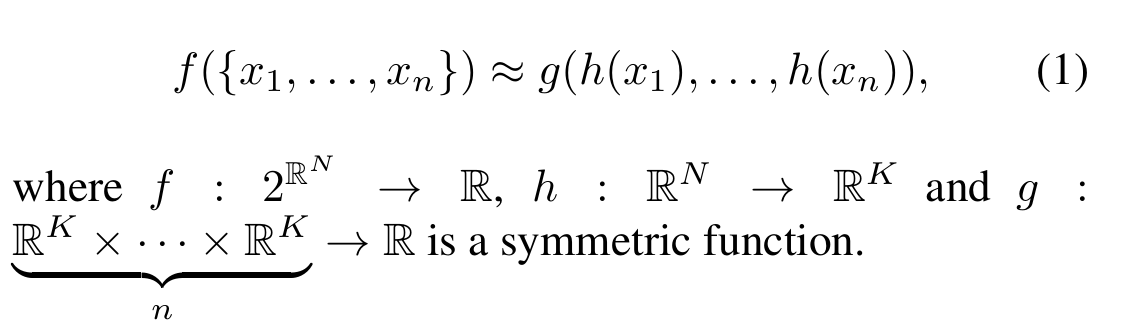
函数f是我们期待得到的分类结果,h函数是为了将单个点x的特征映射到高维,从而提取出单个点的特征,函数g则是对称函数,假设是Max pooling,则就可以在一组单个点的特征中提取出最显著的特征,以此来逼近函数f的效果(输入一组无序数据,然后得到一个结果)。
(2)局部特征与全局特征结合
如PointNet结构中分割网络那一部分所示,将全局特征与经过一层MLP得到的特征进行结合,方法是将全局特征拼接在每一个点的向量的后面,构成了带有局部与全局的结果,再对这些结果进行分割,原因就是分割需要知道局部与全局的特征。
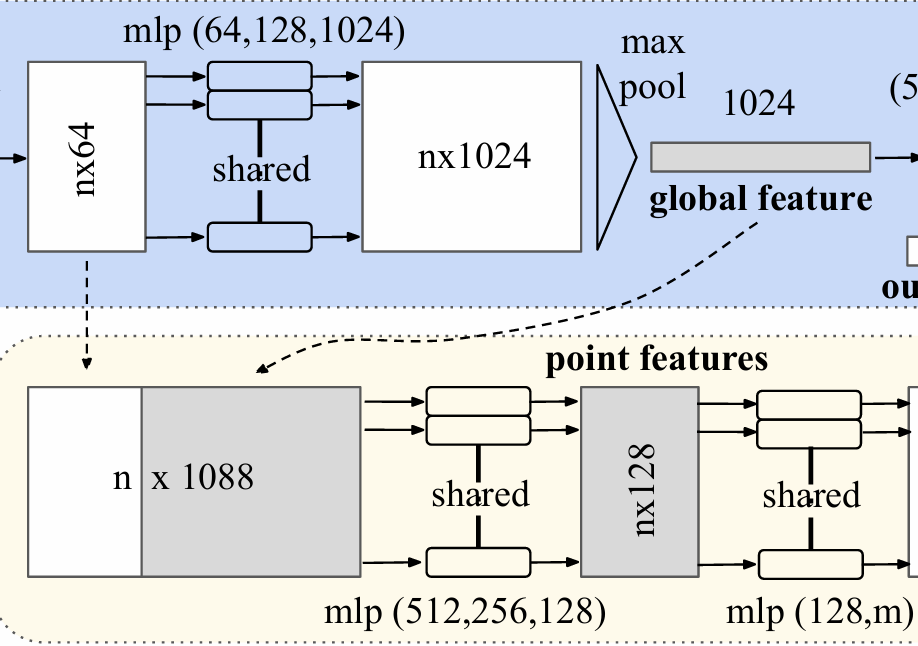
(3)联合对齐网络(Joint Alignment Network)
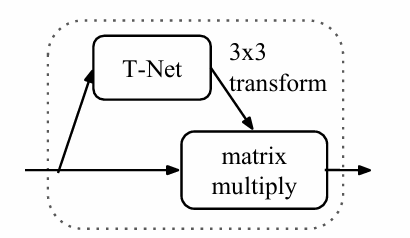
这个网络存在的意义是为了将点云数据按照一定的标准规范进行对齐,以便于后续模型进行学习。所谓T-Net,按照Gemini的解释,T-Net 是一个微型 PointNet ,将原始的数据输入T-Net后,得到一个3*3的变换矩阵,这个矩阵可以将当前的原始点云数据进行刚性变换(旋转),以达到规范的方向。
那么这个标准或者规范是什么呢?Gemini如此说:T-Net 在 PointNet 中将数据按照**“标准”对齐**,这里的“标准”并不是一个固定的、人为预设的坐标系,而是网络在训练过程中自己学习到的、对分类任务最有利的“规范化空间”。简单来说,这个“标准”是一个**数据驱动(Data-Driven)**的、**内隐(Implicit)**的标准。因此,这个标准是模型自己学习到的,而非人为固定。
如何学习?作者给出了一个损失函数:
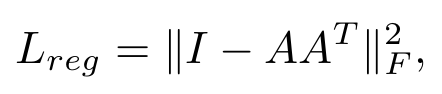
I是单位矩阵,A是通过T-Net学习到的变换矩阵,为了保证实现刚性变换,A尽可能是一个正交矩阵,我们知道正交矩阵与自己相乘的结果是一个单位矩阵。因此上图中这个减法其实就是“理想与现实的差距”,而我们把这个差距作为损失。$$||\cdot||_F$$ 表示 Frobenius 范数,公式为:
$$\|M\|_F = \sqrt{\sum_{i=1}^m \sum_{j=1}^n |M_{ij}|^2}$$
五、总结
这篇文章我并没有看完,只是看了这个模型的基本思想和运作原理,当然对于为什么要这样我其实也不是完全懂。PointNet就先到这里,后面开始看PointNet++的文献。

