小批量,也称为mini-batch,一般来说,数据集超过1500以上就可以实践mini-batch。这一过程实际上是将大量数据按照一定的小规模进行分批,比如有50000个数据样本,按照1000为单位,将50000分为50个mini-batch,每个mini-batch有1000个数据样本。
一、前向传播
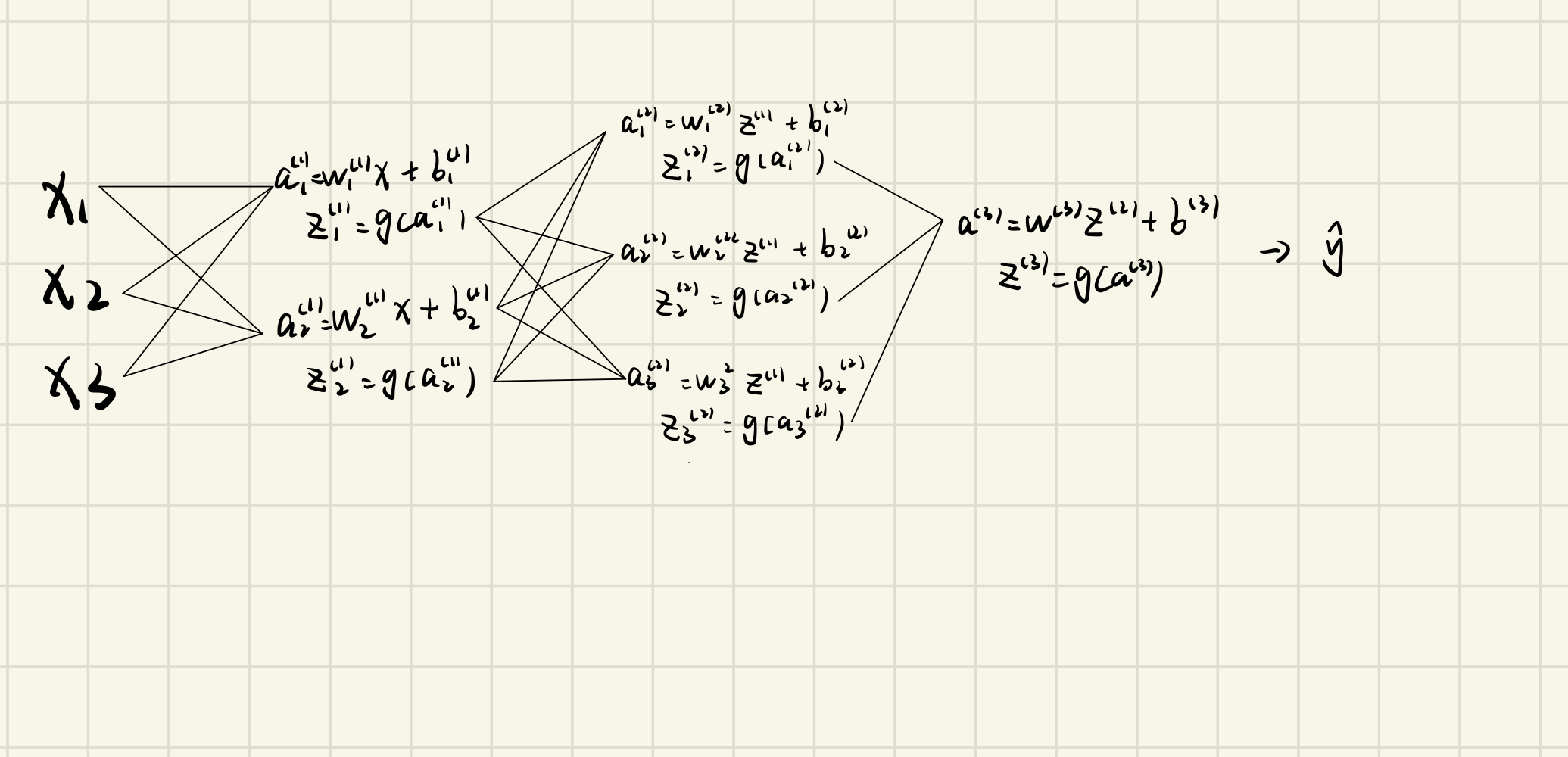
小批量梯度下降,实际上就是在每一个mini-batch上进行梯度下降,参数在batch之间传递。下图是前向传播的过程,神经网络的模型是一元线性回归,激活函数是sigmoid。

因此,神经网络的参数为w、b,在训练开始前需要为每一层每一个神经元赋予初始参数值。某一batch全部通过神经网络后,接下来开始反向传播(backforward propagation)
二、反向传播(backforward propagation)
反向传播实际上就是计算链式偏导数,在下面的模型中,前一层的结果会传递到后一层,后一层的结果又会传递到更下一层,因此关系是层层嵌套,到最后的输出层时,Z(3)里面包含了前两层的全部参数,因此可以链式求偏导至每层每个神经元,直至第一个隐藏层。
三、梯度下降
下图时神经元内部的模型与激活函数,以及损失函数与代价函数。

在上述的定义下,简单地构建一个单个神经元的梯度下降过程
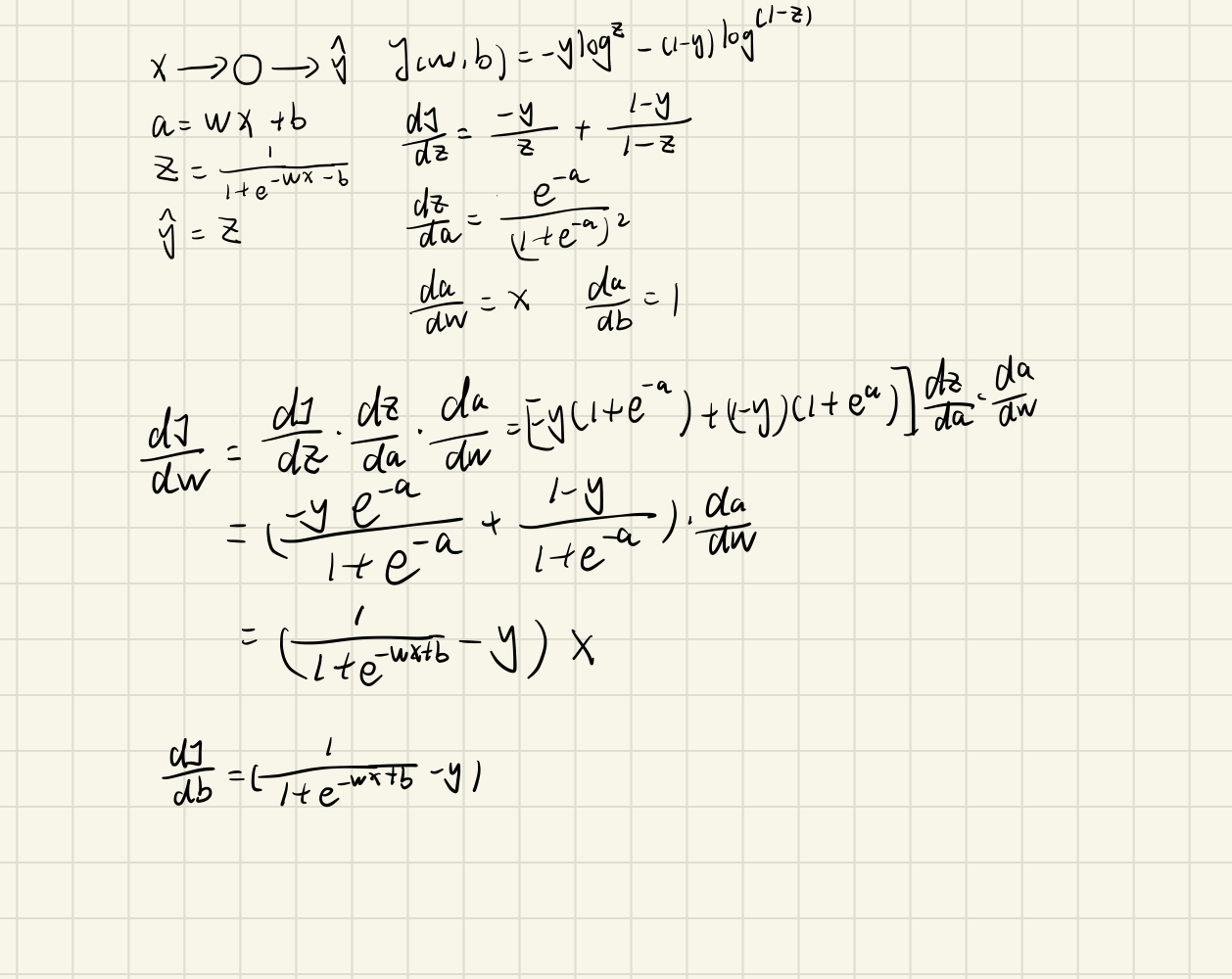
因为只有一个样本x,所以代价函数就是损失函数。为了得到神经元的参数偏导,我们将一步一步链式求导。上图可以看见,分别求偏导后,再将他们相乘即可得到dJ/dw、dJ/db,我这里用的符号不严谨,并不是偏导符号。因此,得到了这两个梯度,于是我们就可以用这个梯度来更新参数:
$$
w = w - \alpha \frac{\partial J}{\partial w}
$$
$$
b = b - \alpha \frac{\partial J}{\partial b}
$$
当然这只是一次更新,在梯度下降时,需要不断循环直到代价函数的值收敛。

